ГОСТ Р ИСО 14644-1-2000 Чистые помещения и связанные с ними контролируемые среды. Часть 1. Классификация чистоты воздуха

ПРИЛОЖЕНИЕ С (обязательное). Статистическая обработка данных о концентрации частиц

ПРИЛОЖЕНИЕ С
(обязательное)

С.1 Пояснение

Данный статистический анализ рассматривает только случайные ошибки (недостаточную точность), а не погрешности неслучайной природы (например, погрешности измерения, связанные с ошибочной калибровкой).

С.2 Алгоритм для вычисления средней концентрации частиц в точке отбора ()

Если в точке берется множество проб, то для определения средней концентрации частиц в точке должно использоваться уравнение

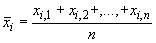, (C.1)

где 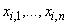- концентрации частиц в отдельных пробах в точке ;

- число проб, взятых в точке .

Вычисление средней концентрации частиц должно быть выполнено для каждой точки пробоотбора, в которой были взяты две или более пробы.

С.3 Алгоритмы для вычисления 95%-ного верхнего доверительного предела

С.3.1 Принцип

Этот метод применим при числе точек пробоотбора, большем и меньшем десяти. В этом случае данная процедура должна использоваться в дополнение к алгоритму, описанному формулой (С.1).

С.3.2 Полное среднее значение средних арифметических значений ()

Полное (итоговое) среднее значение по точкам пробоотбора от среднего арифметического по числу проб вычисляют по формуле

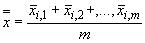, (С.2)

где 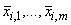- средние для отдельных точек пробоотбора, определенные при помощи формулы (С.1);

- число отдельных средних в каждой точке.

Все средние арифметические в отдельных точках имеют одинаковый вес, независимо от числа проб, взятых в любой данной точке.

С.3.3 Стандартное отклонение среднего (средних) по точкам пробоотбора

Стандартное отклонение средних по точкам пробоотбора определяют по формуле

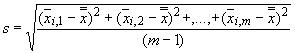, (С.3)

где 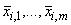- средние для отдельных точек пробоотбора, определенные при помощи формулы (С.1);

- полное (итоговое) среднее значение по точкам пробоотбора от среднего арифметического по числу проб;

- число отдельных средних в каждой точке.

С.3.4 95%-ный верхний доверительный предел (ВДП) для полного среднего значения

95%-ный верхний доверительный предел для полного среднего значения определяют по формуле

95% ВДП= 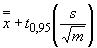, (С.4)

где - полное (итоговое) среднее значение по точкам пробоотбора от среднего арифметического по числу проб;

- 95%-ный процентиль (квантиль) -распределения с -1 степенями свободы;

- число отдельных средних в каждой точке.

Значения квантиля -распределения Стьюдента () для 95%-ного ВДП приведены в таблице С.1. Кроме того, могут использоваться -распределения Стьюдента, имеющиеся в статистических компьютерных программах.


Таблица C.1 - Значения квантиля -распределения Стьюдента для 95%-ного верхнего доверительного предела