

ГОСТ 8032-84
(СТ СЭВ 3961-83)
Группа Т10
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРЕДПОЧТИТЕЛЬНЫЕ ЧИСЛА
И РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Preferred numbers and series of preferred numbers
ОКСТУ 0080
Дата введения 1985-07-01
Постановлением Государственного комитета СССР по стандартам от 9 августа 1984 г. N 2828 срок введения установлен с 01.07.85
ВЗАМЕН ГОСТ 8032-56
ПЕРЕИЗДАНИЕ. Январь 1993 г.
Настоящий стандарт устанавливает предпочтительные числа и ряды предпочтительных чисел, которые должны применяться при установлении градаций и отдельных значений параметров технических объектов (продукции, условий ее существования, технологических процессов и др.), а также ряды чисел (в том числе содержащих непредпочтительные числа), применяемые в случаях, когда использование рядов предпочтительных чисел невозможно или нецелесообразно (далее - предпочтительные ряды чисел).
Стандарт не распространяется на параметры технических объектов, естественная закономерность изменения значений которых отличается от закономерностей образования рядов, установленных настоящим стандартом.
Настоящий стандарт полностью соответствует СТ СЭВ 3961-83.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Предпочтительные числа получают на основе геометрической прогрессии, -й член которой равен
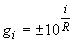
(знаменатель прогрессии 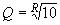 ),
),
где 5, 10, 20, 40, 80 и 160, a
принимает целые значения в интервале от 0 до
.
Значение определяет число членов прогрессии в одном десятичном интервале.
Предпочтительные числа представляют собой округленные значения членов ряда данной прогрессии.
Члены прогрессии, расположенные в интервале от 1,00 до 10,00 составляют исходный ряд.
1.2. Ряды предпочтительных чисел не ограничиваются в обоих направлениях, при этом предпочтительные числа менее 1 и более 10 получают делением или умножением членов исходного ряда на число 10, 100, 1000 и т.д.
1.3. Предпочтительные числа одного ряда могут быть либо только положительными, либо только отрицательными.
1.4. Свойства рядов предпочтительных чисел приведены в приложении 1.