ГОСТ Р 50779.21-2004 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение

8 Точечное и интервальное оценивание доли распределения случайной величины в заданном интервале*

________________
* Доля распределения случайной величины в заданном интервале равна вероятности попадания случайной величины в этот интервал. В большинстве практических задач физический смысл, используемый в данном стандарте, имеет понятие - "доля распределения случайной величины в интервале", хотя все приведенные статистические выводы справедливы и для понятия "вероятность попадания случайной величины в интервал".

8.1 Алгоритм вычисления доли распределения случайной величины в заданном интервале 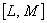и вне его при известных параметрах нормального распределения приведен в таблице 8.1.


Таблица 8.1 - Вычисление доли распределения случайной величины в заданном интервале 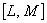и вне его при известных параметрах нормального распределения (вспомогательный алгоритм)

Для решения данной задачи не используют выборочные данные, а значения параметров и считают известными. Таблица 8.1 содержит вспомогательный алгоритм для решения задач по 8.2-8.9.

Пример - Оценка ожидаемого уровня несоответствий показателя качества продукции (уровня несоответствий) при настройке станка на середину поля допуска или на номинальное значение и известную точность .

8.2 Алгоритм точечного оценивания доли распределения случайной величины в заданном интервале 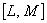и вне его при известном стандартном отклонении или дисперсии приведен в таблице 8.2.


Таблица 8.2 - Точечное оценивание доли распределения случайной величины в заданном интервале 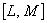и вне его при известном стандартном отклонении или дисперсии

Пример - Оценка уровня несоответствия показателя качества продукции, который следует ожидать при работе станка или технологического процесса при установленном допуске и неизвестном уровне настройки. При этом считают, что точность станка или технологического процесса известна или достаточно точно оценена заранее.

8.3 Алгоритм точечного оценивания доли распределения случайной величины в заданном интервале 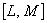и вне его при неизвестной дисперсии приведен в таблице 8.3.


Таблица 8.3 - Точечная оценка доли распределения случайной величины в заданном интервале 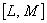и вне его при неизвестной дисперсии

Пример тот же, что в 8.2, но точность станка или технологического процесса неизвестна.

8.4 Алгоритм определения верхней и нижней доверительных границ для доли распределения случайной величины с неизвестной дисперсией в одностороннем интервале и вне его с заданной нижней границей приведен в таблице 8.4.

Указанным в таблице 8.4 способом определяют верхнюю доверительную границу для доли распределения вне одностороннего интервала с нижней границей , а также нижнюю доверительную границу для доли распределения случайной величины в указанном интервале.

Примечание - Здесь и далее следует различать заданный изначально односторонний или двусторонний интервал (допуск) с известной границей (границами) для случайной величины и доверительный интервал для доли распределения случайной величины в этом допуске и вне его. Границы заданного интервала (допуска) и для случайной величины измеряют в тех же единицах величин, какие имеет случайная величина, например: в миллиметрах, граммах и т.п. Границы получаемого доверительного интервала являются безразмерными, как и сама вероятность.


Примеры

1 Определение уровня несоответствий для показателя "толщина гальванопокрытия". Случай, когда необходимо иметь определенную уверенность в том, что уровень несоответствий не превышает установленного предельного процента.

2 Оценка доли годных и несоответствующих деталей по показателю качества "твердость после термической обработки". Требование (допуск) одностороннее: =45 ед. Роквелла. Оценка получается в виде верхней доверительной границы на долю несоответствующей продукции с твердостью ниже 45 ед. Кроме того, получается нижняя доверительная граница на долю продукции, соответствующей требованию, т.е. на долю деталей с твердостью не ниже 45 ед. Доверительные оценки и в отличие от точечных имеют характеристики достоверности утверждений (с вероятностью 1-):

истинная доля годной продукции - не менее ;

истинная доля несоответствующей продукции - не более .


Таблица 8.4 - Определение верхней и нижней доверительных границ для доли распределения случайной величины в одностороннем интервале и вне его с заданной нижней границей (дисперсия неизвестна)

Следующая глава