ГОСТ Р 50779.21-96 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение

4 ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ

- математическое ожидание нормального закона распределения (среднее значение генеральной совокупности);

Примечание - Далее по тексту - среднее значение.


- известное значение параметра ;

, - математические ожидания для двух различных генеральных совокупностей;

- точечная оценка параметра ; .

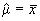, - верхняя и нижняя доверительные границы параметра ;

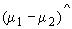- точечная оценка разности значений параметров и ;

- стандартное (среднее квадратическое) отклонение нормально распределенной случайной величины;

- дисперсия генеральной совокупности, ;

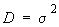- известное значение дисперсии генеральной совокупности, ;

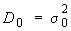- конкретное численное значение параметра ;

, - известные значения параметров и для двух генеральных совокупностей;

- точечная оценка параметра , ;

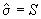, - верхняя и нижняя доверительные границы параметра ;

- точечная оценка дисперсии;

- выборочное значение наблюдаемой случайной величины;

- выборочное значение случайной величины из первой генеральной совокупности;

- то же, из второй генеральной совокупности;

, , - объемы выборок;

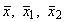- средние арифметические значения (выборочные средние);

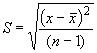- выборочное стандартное (среднее квадратическое) отклонение;

, - то же, для двух выборок соответственно;

- риск первого рода (вероятность отвергнуть гипотезу, когда она верна);

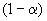- доверительная вероятность, где , 0 << 1, - уровень значимости при проверке гипотез;

- число степеней свободы;

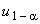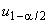, - квантили стандартного нормального закона распределения уровней и соответственно;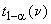

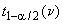, - квантили распределения Стьюдента с степенями свободы уровней и 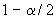соответственно;

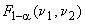- квантиль распределения Фишера уровня с и степенями свободы;

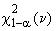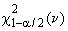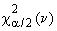, , - квантили -распределения c степенями свободы уровне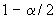й , и соответственно;

, - нижняя и верхняя границы заданного интервала;

- доля распределения (вероятность попадания) случайной величины в заданном интервале [, ];

- доля распределения (вероятность попадания) случайной величины вне интервала [, ], причем ;

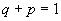- точечные оценки и ;

, - нижние односторонние доверительные границы для и ;

, - верхние односторонние доверительные границы для и ;

- случайное событие, например: попадание случайной величины в заданный интервал;

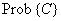- вероятность случайного события ;

- сумма выборочных значений .