Доверительный интервал для среднего совокупности вычисляют на основе оценок среднего и стандартного отклонения.
Альтернативный метод вычисления доверительного интервала с использованием размахов дан в приложении А.
6.1 Оценка стандартного отклонения
6.1.1 Случай несгруппированных результатов
Оценку 
стандартного отклонения 
, вычисляемую на основе квадратов отклонений от среднего арифметического, задают формулой
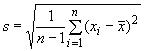, (4)
где 
- значение 
-го измерения (
1, 2, 3,... 
); - общее число измерений; 
- среднее арифметическое измерений, вычисленное по формуле (1).
Для упрощения вычислений рекомендуется использовать формулу
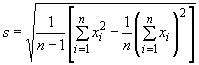. (5)
6.1.2 Случай сгруппированных результатов
В случае группирования в классы формула для оценки стандартного отклонения имеет вид
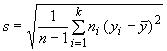, (6)
где 
- средняя точка в -м классе (1, 2, 3, ... 
); - число классов; - общее число измерений;
- взвешенное среднее всех средних точек классов, вычисленное по формуле (3).
Для простоты вычислений рекомендуется использовать формулу
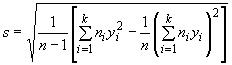. (7)
В случае сгруппированных данных вычисленное значение может быть скорректировано (поправка Шеппарда). Поскольку эта поправка при правильно выбранной ширине класса невелика, ее вводят не всегда.
6.2 Доверительный интервал для среднего
Доверительный интервал определяется тем, какая выбрана доверительная вероятность 
(0,95 или 0,99), и тем, какой будет построен интервал (односторонний или двусторонний).
6.2.1 Двусторонний доверительный интервал
Двусторонний доверительный интервал для среднего 
совокупности определяют по следующим формулам:
а) для доверительной вероятности 0,95:
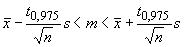; (8)
б) для доверительной вероятности 0,9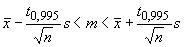9:
. (9)
6.2.2 Односторонний доверительный интервал
Односторонний доверительный интервал для среднего совокупности определяют по одной из следующих формул:
а) для доверительной вероятности 0,95:
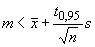(10)
или
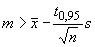; (11)
б) для доверительной вероятности 0,99:
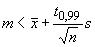(12)
или
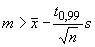. (13)
При этом , если необходимо, может быть заменен на в случае сгруппированных в классы результатов.
Здесь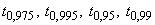 
- квантили распределения Стьюдента c 
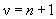степенями свободы.
Их значения даны в таблице 1. В таблице 1 указаны также значения отношений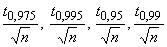 
.
Таблица 1 - Значения 
и отношения 
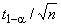для одностороннего доверительного интервала и значения 
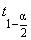и отношения 
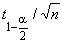(для двустороннего доверительного интервала.
|
Доверительная вероятность для двустороннего доверительного интервала |
Доверительная вероятность для одностороннего доверительного интервала |
|
Доверительная вероятность для двустороннего доверительного интервала |
Доверительная вероятность для одностороннего доверительного интервала |
||||
0,95 |
0,99 |
0,95 |
0,99 |
0,95 |
0,99 |
0,95 |
0,99 |
||
|
|
|
|
|
|
|
|
||
2 |
12,71 |
63,66 |
6,314 |
31,82 |
2 |
8,985 |
45,013 |
4,465 |
22,501 |
3 |
4,303 |
9,925 |
2,920 |
6,965 |
3 |
2,484 |
5,730 |
1,686 |
4,021 |
4 |
3,182 |
5,841 |
2,353 |
4,541 |
4 |
1,591 |
2,920 |
1,177 |
2,270 |
5 |
2,776 |
4,604 |
2,132 |
3,747 |
5 |
1,242 |
2,059 |
0,953 |
1,676 |
6 |
2,571 |
4,032 |
2,015 |
3,365 |
6 |
1,049 |
1,646 |
0,823 |
1,374 |
7 |
2,447 |
3,707 |
1,943 |
3,143 |
7 |
0,925 |
1,401 |
0,734 |
1,188 |
8 |
2,365 |
3,499 |
1,895 |
2,998 |
8 |
0,836 |
1,237 |
0,670 |
1,060 |
9 |
2,306 |
3,355 |
1,860 |
2,896 |
9 |
0,769 |
1,118 |
0,620 |
0,966 |
10 |
2,262 |
3,250 |
1,833 |
2,821 |
10 |
0,715 |
1,028 |
0,580 |
0,892 |
11 |
2,228 |
3,169 |
1,812 |
2,764 |
11 |
0,672 |
0,956 |
0,546 |
0,833 |
12 |
2,201 |
3,106 |
1,796 |
2,718 |
12 |
0,635 |
0,897 |
0,518 |
0,785 |
13 |
2,179 |
3,055 |
1,782 |
2,681 |
13 |
0,604 |
0,847 |
0,494 |
0,744 |
14 |
2,160 |
3,012 |
1,771 |
2,650 |
14 |
0,577 |
0,805 |
0,473 |
0,708 |
15 |
2,145 |
2,977 |
1,761 |
2,624 |
15 |
0,554 |
0,769 |
0,455 |
0,668 |
16 |
2,131 |
2,947 |
1,753 |
2,602 |
16 |
0,533 |
0,737 |
0,438 |
0,651 |
17 |
2,120 |
2,921 |
1,746 |
2,583 |
17 |
0,514 |
0,708 |
0,423 |
0,627 |
18 |
2,110 |
2,898 |
1,740 |
2,567 |
18 |
0,497 |
0,683 |
0,410 |
0,605 |
19 |
2,101 |
2,878 |
1,734 |
2,552 |
19 |
0,482 |
0,660 |
0,398 |
0,586 |
20 |
2,093 |
2,861 |
1,729 |
2,539 |
20 |
0,468 |
0,640 |
0,387 |
0,568 |
21 |
2,086 |
2,845 |
1,725 |
2,528 |
21 |
0,455 |
0,621 |
0,376 |
0,552 |
22 |
2,080 |
2,831 |
1,721 |
2,518 |
22 |
0,443 |
0,604 |
0,367 |
0,537 |
23 |
2,074 |
2,819 |
1,717 |
2,508 |
23 |
0,432 |
0,588 |
0,358 |
0,523 |
24 |
2,069 |
2,807 |
1,714 |
2,500 |
24 |
0,422 |
0,573 |
0,350 |
0,510 |
25 |
2,064 |
2,797 |
1,711 |
2,492 |
25 |
0,413 |
0,559 |
0,342 |
0,498 |
26 |
2,060 |
2,787 |
1,708 |
2,485 |
26 |
0,404 |
0,547 |
0,335 |
0,487 |
27 |
2,056 |
2,779 |
1,706 |
2,479 |
27 |
0,396 |
0,535 |
0,328 |
0,477 |
28 |
2,052 |
2,771 |
1,703 |
2,473 |
28 |
0,388 |
0,524 |
0,322 |
0,467 |
29 |
2,048 |
2,763 |
1,701 |
2,467 |
29 |
0,380 |
0,513 |
0,316 |
0,658 |
30 |
2,045 |
2,756 |
1,699 |
2,462 |
30 |
0,373 |
0,503 |
0,310 |
0,449 |
40 |
2,024 |
2,707 |
1,682 |
2,430 |
40 |
0,320 |
0,428 |
0,266 |
0,384 |
50 |
2,008 |
2,680 |
1,676 |
2,404 |
50 |
0,284 |
0,379 |
0,237 |
0,340 |
60 |
2,000 |
2,664 |
1,673 |
2,393 |
60 |
0,258 |
0,344 |
0,216 |
0,309 |
Если значения больше 60, предпочтительно вычислять значения 
линейной интерполяцией 
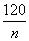, используя таблицу 2.
Таблица 2 -Значения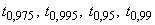 
при 
60
|
|
|
|
|
|
60 |
2 |
2,00 |
2,664 |
1,673 |
2,393 |
120 |
1 |
1,980 |
2,617 |
1,658 |
2,358 |
|
0 |
1,960 |
2,576 |
1,645 |
2,326 |
Пример: 
250;
;
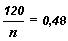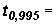2,576+0,48x(2,617-2,576)=2,596.
